Isotopes of an element behave slightly differently during evaporation, condensation, transport and/or reactions, processes which all lead to isotope fractionation. Most simply, fractionation considers the ratio of two isotopes in two species or two phases at equilibrium, which implies that the ratio is constant among the phases or species. The ratio may grow and change 1) in separation processes where the product is removed from the reactant (Rayleigh fractionation), 2) with the progress of chemical reactions and 3) during diffusion.
The Runge-Kutta integration procedure of PHREEQC and the flexible
input formats allow to calculate isotope fractionation. The first example
simulates oxygen fractionation during condensation of vapor in a Rayleigh
process, the next is about 13C fractionation in precipitating calcite under
varying conditions.
Details on the calculations are available in Appelo and Postma (2005) and in Appelo,
2002; 98 kB pdf).
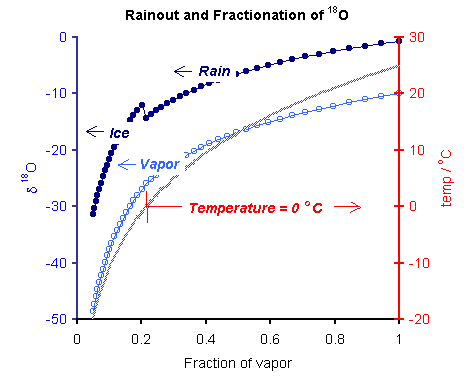
Fractionation of 18O during cooling of water vapor from an initial temperature of 25oC to -20oC with condensation of rain and subsequently of ice. PHREEQC input file istp1.phr

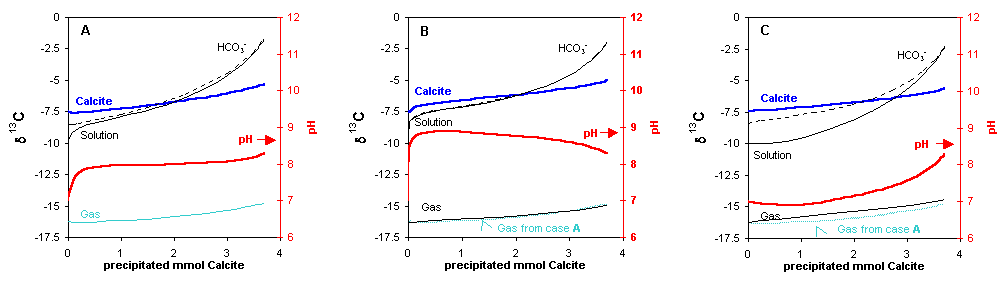
We start with a 5 mM Ca(HCO3)2 solution. Initial pH = 7, solution δ13C = -10‰. In A, the rates for degassing and for calcite precipitation approach equilibrium at the same pace. In B, the rate for CO2 degassing is 100 fold greater than in A, in C, the rate for calcite precipitation is 100 fold greater than in A. The different (relative) rates lead to subtle changes in the isotope compositions. In B and C, the trace of δ13C in gas from A is shown with a dotted line for comparison. Note that at high pH (case B), δ13C of the solution (full line) and of HCO3- (dotted line) coincide.Input file istp2.phr
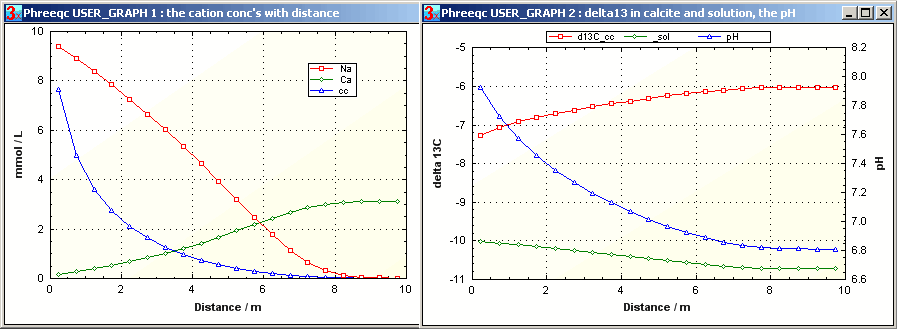
For modeling 13C fractionation during transport, the isotope should be introduced as a separate species in PHREEQC. For example, we imagine a flowline where a NaHCO3 solution displaces CaCl2 solution, and where cation exchange of Na+ for Ca2+ induces supersaturation and precipitation of calcite. The figure indicates the decrease of the Na concentration along the flowline due to exchange with Ca. Part of the released Ca precipitates in calcite, so that the sum of the cations (in meq/L) also decreases. The fractionation of 13C into calcite lightens the solution, but still, the calcite turns heavier along the flowline because the pH decreases in response to precipitation of calcite. PHREEQC input file istp3.phr